Das Camp konnte nun schon zum neunten Mal, durch die Zusammenarbeit zwischen der Leipziger Schülergesellschaft für Mathematik e.V. und dem Thüringer Mathematikolympiadekomitee in Ilmenau, durchgeführt werden. Insgesamt nahmen 78 Schülerinnen und Schüler der Klassenstufen 5 bis 12 teil.

Natürlich stand die Mathematik im Vordergrund. So wurde an allen Tagen über mathematische Fragestellungen diskutiert. Im Eröffnungsvortrag sprach Prof. Dr. Hans-Gert Gräbe (Leipzig) über reguläre Polyeder. Weiter wurden u.a. folgende Themen angeboten: Zahlentheorie, Vollständige Induktion, Geometrie, Zahlenfolgen, Inversion am Kreis, rekursive Folgen, Graphentheorie, Wahrscheinlichkeitsrechnung, Körper und ihre Netze, Platonische Körper, Eulerscher Polyedersatz, Schubfachschluß, konvexe und konkave Funktionen, Jensensche Ungleichung mit Anwendungen, Ungleichungen, Beweise mit Mittelungleichungen. Große Resonanz fand ein Sudokuturnier. Die Teilnehmer hatten 20 Sudokus in vorgegebener Zeit zu lösen.

Das Freizeitangebot wurde wieder rege wahrgenommen. Organisiert wurden ein Skat-, ein Blitzschach- und ein Tischtennisturnier, eine Ganztagswanderung, die die einzelnen Gruppen in den Thüringer Wald führte, eine Nachtwanderung mit anschließendem Grillen und es gab die Möglichkeit zum Rudern und zum Besuch des Schwimmbads. Sportliche Betätigungen wie Fußball, Basketball (zumeist als Frühsport), Tischtennis oder Volleyball gehörten ebenfalls zum Programm. Schließlich waren einige Betreuer und Schüler in den letzten beiden Tagen mit der Produktion leckerer Kuchen und Torten befasst.

Die Schülerinnen und Schüler erhielten eine „Aufgabe des Tages”, die täglich ausgewertet wurde. Die Schüler reagierten hierauf täglich mit einer „Aufgabe der Nacht”. Obligatorisch war natürlich die Durchführung einer Lagerolympiade in Form einer dreistündigen Klausur.

Über die Jahre hinweg ist es gelungen, die besten Schüler für dieses Camp zu interessieren. So nahmen in diesem Jahr drei erste Preisträger und fünf zweite Preisträger der vierten Stufe der Mathematik-Olympiade in München aus den Ländern Sachsen und Thüringen teil. Den Teilnehmern hat das diesjährige Mathecamp wieder so gut gefallen, dass fast alle im nächsten Jahr wiederkommen wollen.

Die Betreuung der Schülerinnen und Schüler erfolgte – z.T. zeitweise – durch Jens Albrecht, Kirstin Ciesinger, Hans-Gert Gräbe, Steffen Hintze, Niels Krap, Susanne Kürsten, Wolfgang Moldenhauer, Anja Pruchnewski, Sven Prüfer, Tobias Schoel, Uwe Schulze, Axel Schüler, Holger Täubig und Alexander Unger.

Eine Aufgabe des Tages

In jedes der 6 × 6 Felder im abgebildeten Gitter ist ein „Haus” der Höhe 1 bis 6 so einzutragen, dass in jeder Zeile und in jeder Spalte jede Zahl genau einmal vorkommt. Die Zahlen am Rand geben an, wie viele Häuser von dieser Seite aus zu sehen sind; ein Haus kann nicht gesehen werden, wenn ein höheres Haus davor steht.

Ein Beispiel für ein 4 × 4-Quadrat (siehe Titelbild – dort um 180° gedreht):

⇒

Versuchen Sie zunächst eine und dann vielleicht auch alle Lösungen zu finden!

Ein weiteres Problem

Man beweise: Zu jeder 100-stelligen Zahl M kan man eine Zahl finden, die durch 1989 teilbar ist und deren letzte 100 Ziffern die Zahl M bilden.

Veruchen Sie zunächst selbst eine Lösung zu finden. Danach können Sie die Lösungen der Schüler lesen.

Achtung hier kommen gleich die Lösungen.

Von Lisa Sauermann:

Eine solche Zahl ist M · 1989^φ(10100). Nach dem Euler-Fermatschen Satz ist wegen kgV(1989,10) = 1 nämlich 1989^φ(10100) ≡ 1 mod 10¹⁰⁰.

Von Georg Schröter:

Eine solche Zahl ist M · (∑_i=0…8 10¹⁰⁰ⁱ)(10¹⁰⁵+1)(10¹⁰⁴+1). Die erste Klammer ist durch 9, die zweite durch 13 und die dritte durch 17 teilbar. Wegen 9 · 13 · 17=1989 ist die Teilbarkeit durch 1989 nachgewiesen. Dass die letzten 100 Ziffern mit M übereinstimmen ist leicht zu sehen.

Aufgaben aus der Lagerolympiade Klasse 9-11

1. Bestimme die Einerziffer von (2+√3)²⁰⁰⁶.
2. Ermittle alle positiven reellen Zahlen a, b, c und d, die das folgende Gleichungssystem erfüllen:

   a + 1/b = 3
   b + 1/c = 4/3
   c + 1/d = 3
   d + 1/a = 4/3
   

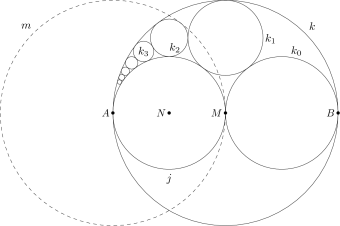
3. Gegeben sei ein Kreis k(M,2) vom Radius 2 mit Mittelpunkt M und ein ihn von innen in A berührender Kreis j(N,1) vom Radius 1. Es sei k₀ der Kreis mit dem Radius 1, der k von innen und j von außen berührt. Ferner sei k_n, n=1,2,… eine rekursiv definierte Folge von Kreisen, die alle k von innen, j von außen und k_n−1 von außen berühren. Berechne den Radius r_n von k_n. Hinweis: Betrachte die Spiegelung am Kreis m(A,2).
   
4. Zusatzaufgabe: Zeige dass für alle ganzen Zahlen a, b, c gilt

   a² + b² + c² ≥ ab + bc + ca + a − b .